| 1. |
Точка на гипотенузе, равноудаленная
от обоих катетов, делит гипотенузу
на отрезки длиной 30 и 40 см. Найдите катеты
треугольника. |
 |
| 2. |
В прямоугольном треугольнике
биссектриса острого угла делит противоположный
катет на отрезки длиной 4 и 5 см.
Определить площадь треугольника. |
 |
| 3. |
Основание равнобедренного треугольника
равно 4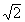 см,
а медиана боковой стороны 5 см. Найти
длины боковых сторон. см,
а медиана боковой стороны 5 см. Найти
длины боковых сторон. |
 |
| 4. |
Найти площадь равнобедренного
треугольника, если основание его равно a, а длина высоты,
проведенной к основанию, равна длине отрезка, соединяющего середины основания
и боковой стороны. |
 |
| 5. |
Длина основания треугольника равна 36 см. Прямая, параллельная основанию,
делит площадь треугольника пополам,
Найти длину отрезка этой прямой, заключенного между сторонами треугольника. |
 |
| 6. |
Основание треугольника равно 30 см, а боковые стороны 26 и 28 см. Высота
разделена в отношении 2 : 3 (считая от вершины), и через точку деления
проведена прямая, параллельная основанию. Определить площадь
полученной при этом трапеции. |
 |
| 7. |
Хорда окружности
равна 10 см. Через один конец хорды проведена
касательная к окружности,
а через другой — секущая, параллельная
касательной. Определить радиус
окружности, если внутренний отрезок секущей
равен 12 см. |
 |
| 8. |
Через концы дуги окружности, содержащей 120°, проведены касательные,
и в фигуру, ограниченную этими касательными
и данной дугой, вписана окружность. Доказать, что ее длина равна длине
исходной дуги. |
 |
| 9. |
Дана точка P, удаленная на 7 см от центра
окружности радиуса 11 см. Через эту точку проведена хорда
длиной 18 см. Каковы длины отрезков, на которые делится хорда
точкой P? |
 |
| 10. |
Три окружности разных радиусов попарно
касаются друг друга. Прямые, соединяющие их центры, образуют прямоугольный
треугольник. Найти радиус меньшей окружности,
если радиусы большей и средней окружностей
равны 6 и 4 см. |
 |
| 11. |
Сторона равностороннего треугольника,
вписанного в окружность, равна a.
Вычислить площадь отсекаемого ею сегмента. |
 |
| 12. |
Круг разделен на два сегмента хордой,
равной стороне правильного вписанного
треугольника. Определить отношение площадей этих сегментов. |
 |
| 13. |
Каждая из трех равных окружностей
радиуса r касается двух других. Найти площадь
треугольника, образованного общими внешними касательными
к этим окружностям. |
 |
| 14. |
Радиус окружности, описанной
около прямоугольного треугольника,
относится к радиусу вписанной в него
окружности как 5 : 2. Найти площадь
треугольника, если один из его катетов равен a. |
 |
| 15. |
Найти радиус окружности, описанной
около прямоугольного треугольника,
если радиус окружности, вписанной
в этот треугольник, равен 3 см, а один из катетов равен 10 см. |
 |
| 16. |
Найти площадь круга, вписанного
в прямоугольный треугольник, если
высота, проведенная к гипотенузе, делит
последнюю на отрезки длиной 25,6 и 14,4 см. |
 |
| 17. |
В равнобедренном треугольнике
основание равно 30 см, а боковая сторона равна 39 см. Определить радиус
вписанного круга. |
 |
| 18. |
К окружности, вписанной в равнобедренный
треугольник с основанием 12 см и высотой 8 см, проведена касательная,
параллельная основанию. Найти длину отрезка этой касательной,
заключенного между сторонами треугольника. |
 |
| 19. |
В окружность, диаметр которой равен
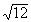 ,
вписан правильный треугольник. На
его высоте как на стороне построен другой правильный треугольник, в который‚
вписана новая окружность. Найти радиус этой окружности. ,
вписан правильный треугольник. На
его высоте как на стороне построен другой правильный треугольник, в который‚
вписана новая окружность. Найти радиус этой окружности. |
 |
| 20. |
В равносторонний треугольник
вписана окружность. Этой окружности
и сторон треугольника касаются три малые окружности. Найти сторону треугольника,
если радиус малой окружности равен r. |
 |
| 21. |
Стороны треугольника равны 13, 14 и 15 см. Найти отношение площадей
описанного и вписанного
в треугольник кругов. |
|
| 22. |
Сторона правильного треугольника,
вписанного в окружность, равна a. Вычислить площадь квадрата,
вписанного в ту же окружность. |
|
| 23. |
Площадь равнобедренного
треугольника равна 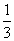 площади квадрата, построенного на основании
данного треугольника. Длины боковых сторон треугольника короче длины его
основания на 1 см. Найти длины сторон и высоты
треугольника, проведенной к основанию.
площади квадрата, построенного на основании
данного треугольника. Длины боковых сторон треугольника короче длины его
основания на 1 см. Найти длины сторон и высоты
треугольника, проведенной к основанию. |
 |
| 24. |
В квадрат вписан другой квадрат,
вершины которого лежат на сторонах первого, а стороны составляют со сторонами
первого углы в 60°. Какую часть площади данного квадрата
составляет площадь вписанного? |
 |
| 25. |
Сторона квадрата, вписанного в окружность,
отсекает сегмент, площадь которого равна
(2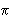 -
4) см2. Найти площадь квадрата. -
4) см2. Найти площадь квадрата. |
|
| 26. |
В прямоугольный треугольник с
углом 60° вписан ромб со стороной, равной
6см, так, что угол в 60° у них общий и все вершины ромба
лежат на сторонах треугольника. Найти стороны треугольника. |
 |
| 27. |
Периметр ромба равен 2 м, длины его
диагоналей относятся как 3 : 4. Найти площадь ромба. |
 |
| 28. |
Высота ромба, проведенная из вершины
тупого угла, делит его сторону на отрезки длиной m и n (m
считать от вершины острого угла). Определить диагонали ромба. |
 |
| 29. |
В ромб, который делится своей диагональю
на два равносторонних треугольника,
вписана окружность радиуса 2. Найти сторону ромба. |
 |
| 30. |
Величина одного из углов параллелограмма
равна 60°, а меньшая диагональ 2 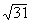 см. Длина перпендикуляра, проведенного из точки пересечения диагоналей
к большей стороне, равна
см. Длина перпендикуляра, проведенного из точки пересечения диагоналей
к большей стороне, равна 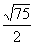 см. Найти длины сторон и большей диагонали параллелограмма.
см. Найти длины сторон и большей диагонали параллелограмма. |
 |
| 31. |
В точках пересечения двух окружностей с радиусами 4 и 8 см касательные
к ним взаимно перпендикулярны. Вычислить площадь фигуры O1ABO2,
где AB — общая касательная к окружностям, а O1
и O2 — их центры. |
 |
| 32. |
Длины оснований трапеции равны 25
и 4 см, а длины боковых сторон — 20 и 13 см. Найти высоту трапеции. |
 |
| 33. |
В трапеции, площадь
которой равна 594 м2, высота 22 м, а разность длин оснований
равна 6 м, найти длины оснований. |
|
| 34. |
Вычислить площадь прямоугольной
трапеции, если ее острый угол равен
60°, меньшее основание равно a, а больная боковая сторона равна
b. |
|
| 35. |
Диагональ равнобедренной
трапеции делит ее тупой угол пополам. Меньшее основание трапеции равно
3 см, периметр равен 42 см. Найти площадь
трапеции. |
 |
| 36. |
Найти диагональ и боковую сторону равнобедренной
трапеции с основаниями 20 и 12 см, если известно, что центр описанной
окружности лежит на большем основании трапеции. |

|
| 37. |
Найти площадь равнобедренной
трапеции, если высота равна h, а боковая сторона видна из центра
описанной окружности под
углом 60°. |
 |
| 38. |
Площадь равнобедренной трапеции,
описанной около круга, равна S. Определить боковую сторону трапеции,
если угол при основании трапеции равен 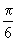 . . |
|
| 39. |
В равнобедренную трапецию
вписан круг. Одна из боковых сторон делится точкой касания
на отрезки длиной m и n. Определить площадь
трапеции. |
 |
| 40. |
Вычислить отношение площадей
квадрата, правильного
треугольника и правильного шестиугольника, вписанных в одну и ту же
окружность. |
|
 Задачи
Задачи Задачи
Задачи