п.3.6 Движение в пространстве Минковского.
Введем в пространстве М аффинную систему координат
{xi}, i=1,..,4, фиксируя некоторую точку в качестве начала.Тогда метрика представляется в виде:
ds2=(dx1)2-(dx2)2-(dx3)2-(dx4)2. (3.5)
Из определения движения (3.2) следует, что при движениях коэффициенты этой дифференциальной формы должны оставаться неизменными. Известно, что группа движения пространства Минковского десятипараметрична, она включает 3 вращения, 3 псевдовращения и 4 сдвига по осям, и её называют группой
Пуанкаре или неоднородной группой Лоренца.Её генераторы имеют вид:
бусты (сдвиги):
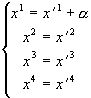 (3.6)
(3.6)
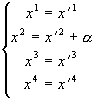 (3.7)
(3.7)
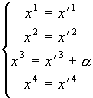 (3.8)
(3.8)
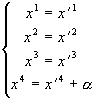 (3.9)
(3.9)
вращения
: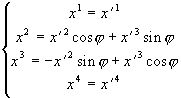 (3.10)
(3.10)
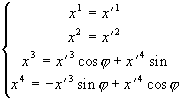 (3.11)
(3.11)
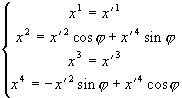 (3.12)
(3.12)
псевдовращения
: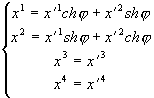 (3.13)
(3.13)
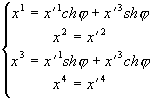 (3.14)
(3.14)
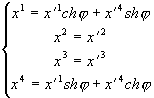 (3.15)
(3.15)
Докажем, что данные преобразования являются движениями в пространстве Минковского.
Рассмотрим
: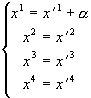 (3.6)
(3.6)
Подставим (3.6) в нашу дифференциальную форму (3.5), получим:
ds2=(d(x¢ 1 + a ))2 - (dx¢ 2)2 - (dx¢ 3)2 - (dx¢ 4)2 = (dx¢ 1 + 0)2 - (dx¢ 2)2 - (dx¢ 3)2 - (dx¢ 4)2 = (dx¢ 1)2 - (dx¢ 2)2 - (dx¢ 3)2 - (dx¢ 4)2.
Для (3.10) имеем
:ds2 = (dx¢ 1)2 - (d(x¢ 2cosj + x¢ 3sinj ))2 - (d( - x¢ 2sinj + x¢ 3cosj )2 - (dx¢ 4)2 = (dx¢ 1)2 - cos2j (dx¢ 2)2 - 2cosj sinj (dx¢ 2dx¢ 3)2 - sin2j (dx¢ 3)2 - cos2j (dx¢ 3)2 + 2cosj sinj (dx¢ 2dx¢ 3)2 - sin2j (dx¢ 2)2 - (dx¢ 4)2 = (dx¢ 1)2 - (cos2j + sin2j )(dx¢ 2)2 - (sin2j +cos2j )(dx¢ 3)2 - (dx¢ 4)2 = (dx¢ 1)2 - (dx¢ 2)2 - (dx¢ 3)2 - (dx¢ 4)2.
Для (3.13) имеем
:ds2 = (d(x¢ 1chj + x¢ 2shj ))2 (dx¢ 1)2 - (d(x¢ 1shj + x¢ 2chj ))2 - (dx¢ 3)2 -(dx¢ 4)2 = ch2j (dx¢ 1)2 + 2chj shj (dx¢ 1dx¢ 2)2 + sh2j (dx¢ 2)2 - sh2j (dx¢ 1)2 - 2shj chj (dx¢ 1 dx¢ 2) - ch2j (dx¢ 2)2 - (dx¢ 3)2 - (dx¢ 4)2 = ch2j (dx¢ 1)2 + sh2j (dx¢ 2)2 - sh2j (dx¢ 1)2 -ch2j (dx¢ 2)2 - (dx¢ 3)2 - (dx¢ 4)2 = (ch2j - sh2j )(dx¢ 1)2 - (ch2j - sh2j )(dx¢ 2)2 -(dx¢ 3)2 - (dx¢ 4)2 = (dx¢ 1)2 - (dx¢ 2)2 - (dx¢ 3)2 - (dx¢ 4)2.
Следовательно из определения движения (3.6), (3.10), (3.13) являются движениями. Аналогично можно убедиться, что преобразования (3.7) - (3.9), (3.11), (3.12), (3.14), (3.15) также авляются движениями в пространстве Минковского.
При инфинитезимальном преобразовании считается, угол j мал, то есть j заменяется на d j . Далее делается разложение в ряд Тейлора, пренебрегая членами выше первой степени.
При инфинитезимальном преобразовании из (3.10)
: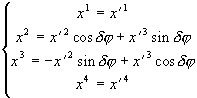
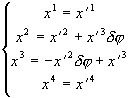 (3.16)
(3.16)
Из (3.11)
: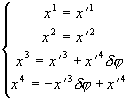 (3.17)
(3.17)
Из (3.12)
: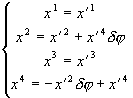 (3.18)
(3.18)
Из (3.13), зная, что
chd j » 1, shd j » d j получаем: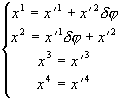 (3.19)
(3.19)
Из (3.14)
: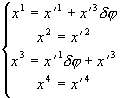 (3.20)
(3.20)
Из (3.15)
: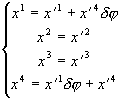 (3.21)
(3.21)
Преобразования (3.16) - (3.21), (3.6) - (3.9) можно переписать в виде
:xi = x¢ i + x i(x)d j ,
где x i соответственно равны:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Векторы
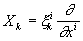 являются генераторами алгебры Ли группы
Пуанкаре. Векторы x
i -
это вектора Киллинга, удовлетворяющие уравнениям Киллинга (3.4).
являются генераторами алгебры Ли группы
Пуанкаре. Векторы x
i -
это вектора Киллинга, удовлетворяющие уравнениям Киллинга (3.4).