п.4.1 Уравнения Киллинга для пространства Минковского.
Матрица для пространства Минковского задается в виде:
gik =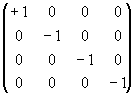 
(4.1)
Используя (4.1) и (3.4) выпишем десять дифференциальных уравнений Киллинга от четырех независимых переменных
xi ,(i = 1,...4).Рассмотрим случай, когда:
1) k = 1, l = 1.
,
,
.
Так как
g11=1g12 = 0
g13 = 0
g14 = 0,
следовательно
(4.2)2) k = 1, l = 2.
g11 = 1 g21 = 0
g12 = 0 g22 = -1
g13 = 0 g23 = 0
g14 = 0 g24 = 0
.(4.3)
3) k = 1, l = 3.
(4.4)
4) k = 1, l = 4.
(4.5)
5) k = 2, l = 2.
(4.6)
6) k = 2, l = 3.
(4.7)
7) k = 2, l = 4.
(4.8)
8) k = 3, l = 3.
(4.9)
9) k = 3, l = 4.
(4.10)
10) k = 4, l = 4.
(4.11)
Получили следующие уравнения Киллинга:
(4.2)
.(4.3)
(4.4)
(4.5)
(4.6)
(4.7)
(4.8)
(4.9)
(4.10)
(4.11)