п.4.3 Нахождение движений по векторам Киллинга.

Используя вектора Киллинга можно найти движения составляющие группу Пуанкаре. Для этого воспользуемся методом, описанным, Картаном [ 1, 188 - 191] .

Так как , и (4.22), то имеем:

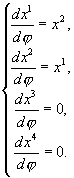
Данная система линейных дифференциальных уравнений эквивалентна:

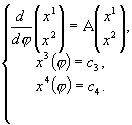
где

Используем стандартный прием решения систем линейных дифференциальных уравнений с постоянными коэффициентами [4, 283].

Имеем (A - l E)a = 0, где E - единичная матрица, а= - собственный вектор с собственным числом l .

Составим матрицу (A - l E)a:

(A - l E)a =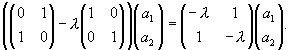

Для определения a₁, a₂ найдем собственное число l из Тогда получаем:

Откуда:

^

Корни последнего уравнения есть l ₁ = 1, l ₂ = -1. При l ₁ = 1 имеем: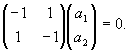

Из последнего равенства получаем -a₁ + a₂ = 0 . Следовательно a₁ = 1, a₂ = 1, то есть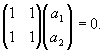 При l ₂ = -1 имеем:

Откуда:

a₁ + a₂ = 0.

Следовательно a₁ = 1, a₂ = -1 , то есть .

Как известно из теории систем линейных дифференциальных уравнений общее решение записывают в данном виде:

.

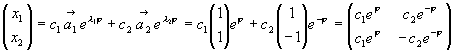Тогда:

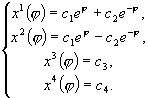
Так как ej = chj + shj

e^-j = chj - shj , то предыдущая система уравнений примет вид: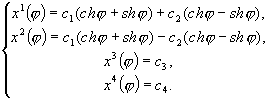

Проводя преобразования в этой системе, получаем окончательное решение системы дифференциальных уравнений:

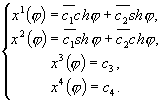
где =c₁ + c₂, = c₁ - c₂.

Используя, что и делая подстановку , , найдем:

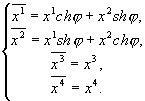
Получили одно из движений группы Пуанкаре, с точностью до переобозначения, являющееся псевдовращением, рассмотренное нами ранее в п.3.6.

Имеем:

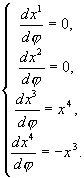
Данная система эквивалентна:

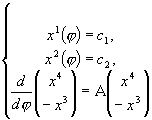
где

Составим матрицу вида (A - l E)a:

(A - l E)a =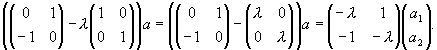

Найдем собственный вектор из Определим для этого l:

имеем

Откуда:

^

Корнями последнего уравнения являются: l ₁ = i, l ₂ = -i. При l ₁ = i имеем: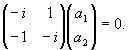

Из последнего равенства получаем -ia₁ + a₂ = 0 . Следовательно a₁ = 1, a₂ = i, то есть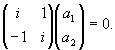 При l ₂ = -i имеем:

Откуда:

ia₁ + a₂ = 0.

Следовательно a₁ = 1, a₂ = -i , то есть .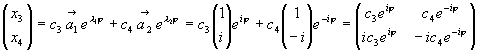

.

Тогда:

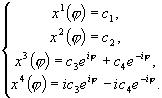
Так как e^ij = cosj + i * sinj

e^-ij = cosj - i * sin , то последняя система примет вид: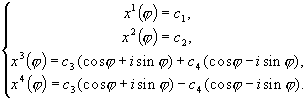

Проводя преобразования в данной системе, получаем окончательное решение:

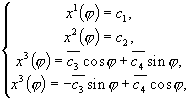
где =c₃ + c₄, =i(c₃ - c₄ ).

Далее, воспользовавшись и делая подстановку , , найдем:

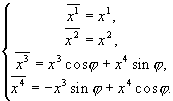
Получили вращение группы Пуанкаре.

Приведенная выше схема рассуждения повторяется для каждого из десяти видов движения.

СОДЕРЖАНИЕ

ДАЛЬШЕ