4.2. Интегрирование уравнений Киллинга

Записывая и интегрируя уравнения Киллинга, полученные в предыдущем пункте этого параграфа, получим вектора Киллинга.

Для этого продифференцируем (4.3) по

Получим:

, так как , то и следовательно .(4.12)

Далее продифференцируем (4.4) по :

, так как , то , следовательно

.(4.13)

Продифференцируем (4.5) по :

, так как , то , следовательно

.(4.14)

Продифференцируем (4.5) по и (4.8) по :

, .

Складывая данные равенства, получаем:

+

---

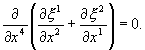
Воспользуемся и подставим данное выражение в предыдущее равенство:

,

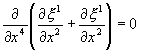(4.15)

Продифференцируем (4.4) и (4.10) соответственно по и :

,

Сложим полученные равенства:

+

---

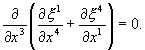
Так как , то

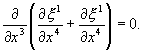
Откуда:

(4.16)

Продифференцируем (4.3) и (4.7) соответственно по и :

,

Сложим эти равенства:

+

---

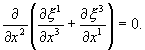
Так как

,

то

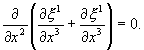
Следовательно

(4.17)

Если выполнены соотношения (4.12) - (4.17), то очевидно, что вектор x ⁱ линейно выражается через координаты, то есть

x ¹ = ax²+bx³+cx⁴+l.(4.18)

Для нахождения остальных x ⁱ рассуждения аналогичны вышеприведенным.

x ² = dx¹+zx³+nx⁴+p.(4.19)

x ³ = mx¹+fx²+gx⁴+h.(4.20)

x ⁴ = kx¹+tx²+sx³+w.(4.21)

Воспользуемся уравнениями Киллинга для уменьшения числа неизвестных коэффициентов в (4.18) - (4.21).

Подставляя (4.18) и (4.19), (4.18) и (4.20), (4.18) и (4.21) , (4.19) и (4.20), (4.19) и (4.21), (4.20) и (4.21) соответственно в (4.3), (4.4), (4.5), (4.7), (4.8), (4.10), получим:

Откуда, проводя данное дифференцирование, находим:

a = d,

b = m,

c = k,

z = -f,

n = -t,

g = -s.

После этого, записывая вектора (4.18) - (4.21), и ,подставляя в них последниe соотношения, получим:

x ¹ = ax² + bx³ + cx⁴ + l,

x ² = ax¹ + zx³ + nx⁴ + p,

x ³= bx¹ - zx²+gx⁴+h,

x ⁴ = cx¹ - nx²- gx³ + w.

Если предположить, что все коэффициенты в x ¹,x ²,x ³,x ⁴ равны нулю, кроме одного, который равен единице, то можно найти десять векторов Киллинга в координатном виде:

1. если a = 1, а все остальные коэффициенты равны нулю, то:

x ¹ = x²,

x ² = x¹,

x ³ = 0,

x ⁴ = 0.

Следовательно

(4.22)

3. если b = 1, а все остальные коэффициенты равны нулю, то:

x ¹ = x³,

x ² = 0,

x ³ = x¹,

x ⁴ = 0.

Следовательно (4.23)

4. если c = 1, а все остальные коэффициенты равны нулю, то:

x ¹ = x⁴,

x ² = 0,

x ³ = 0,

x ⁴ = x¹.

Следовательно (4.24)

5. если z = 1, а все остальные коэффициенты равны нулю, то:

x ¹ = 0,

x ² = x³,

x ³ = -x²,

x ⁴ = 0.

Следовательно (4.25)

6. если n = 1, а все остальные коэффициенты равны нулю, то:

x ¹ = 0,

x ² = x⁴,

x ³ = 0,

x ⁴ = -x².

Следовательно (4.26)

7. если g = 1, а все остальные коэффициенты равны нулю, то:

x ¹ = 0,

x ² = 0,

x ³ = x⁴,

x ⁴ = -x³.

Следовательно (4.27)

8. если l = 1, а все остальные коэффициенты равны нулю, то:

x ¹ = 1,

x ² = 0,

x ³ = 0,

x ⁴ = 0.

Следовательно (4.28)

9. если p = 1, а все остальные коэффициенты равны нулю, то:

x ¹ = 0,

x ² = 1,

x ³ = 0,

x ⁴ = 0.

Следовательно (4.29)

10. если h = 1, а все остальные коэффициенты равны нулю, то:

x ¹ = 0,

x ² = 0,

x ³ = 1,

x ⁴ = 0.

Следовательно (4.30)

11. если w = 1, а все остальные коэффициенты равны нулю, то:

x ¹ = 0,

x ² = 0,

x ³ = 0,

x ⁴ = 1.

Следовательно (4.31)

Векторы (4.22) - (4.31) - это векторы, которые были найдены в п.3.6 используя инфинитезимальные преобразования.

Таким образом, интегрируя уравнения Киллинга можно получить вектора Киллинга в координатном виде.

СОДЕРЖАНИЕ

ДАЛЬШЕ