[Part II, The Electrician, 31, 359 (1893)]
In my first article on this subject (The Electrician, July 14,
1893, р. 281), I partly assumed a knowledge on the part of the reader of
my theory of convective currents of electrification ("Electrical Papers,"
Vol. II., p. 495 and after), and only very briefly mentioned the modified
law of the inverse squares which is involved, viz., with a lateral concentration
of the lines of force. The remarks of the Editor  ,
and of Prof. Lodge
,
and of Prof. Lodge  on gravitational
aberration, lead me to point out now some of the consequences of the modified
law which arises when we assume that the ether is the working agent in
gravitational effects, and that it propagates disturbances at speed v in
the manner supposed in my former article. There is, so far as I can see
at present, no aberrations effect, but only a slight alteration in the
intensity of force in different directions round a moving body considered
as an attractor.
on gravitational
aberration, lead me to point out now some of the consequences of the modified
law which arises when we assume that the ether is the working agent in
gravitational effects, and that it propagates disturbances at speed v in
the manner supposed in my former article. There is, so far as I can see
at present, no aberrations effect, but only a slight alteration in the
intensity of force in different directions round a moving body considered
as an attractor.
 The Electrician,
July 14, p. 277, and July 23, p. 340
The Electrician,
July 14, p. 277, and July 23, p. 340
 The Electrician,
July 28, p. 347
The Electrician,
July 28, p. 347
Thus, take the case of a big Sun and small Earth, of masses 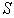 and
and 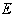 ,
at distance
,
at distance 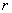 apart. Let
apart. Let 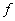 be
the unmodified force of
be
the unmodified force of 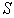 on
on 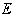 ,
thus
,
thus
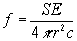 ,
(1)
,
(1)
using rational units in order to harmonise with the electromagnetic
laws when rationally expressed. Also, let 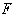 be
the modified force when the Sun is in motion at speed
be
the modified force when the Sun is in motion at speed 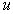 through
the ether. Then
through
the ether. Then 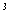
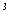 This is the
case of steady motion. There is no simple formula
This is the
case of steady motion. There is no simple formula
when the motion is unsteady
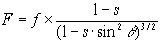 ,
(2)
,
(2)
where 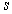 is the small quantity
is the small quantity 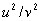 ,
and
,
and 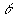 is the angle between
is the angle between 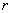 and
the line of motion. ("Electrical Papers," Vol. II., pp. 495, 499).
and
the line of motion. ("Electrical Papers," Vol. II., pp. 495, 499).
Therefore, if the Sun is at rest, there is no disturbance of the Newtonian
law, because its "field of force" is stationary. But if it has a motion
through space, there is a slight weakening of the force in the line of
motion, and a slight strengthening equatorially. The direction is still
radial.
To show the size of the effect, let
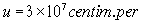
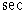
(3)
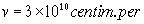
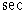
This value of 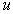 is not
very different from the speed attributed to fast stars, and the value of
is not
very different from the speed attributed to fast stars, and the value of 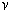 is
the speed of light itself.
is
the speed of light itself.
So we have
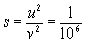 ,
(4)
,
(4)
i.e., one millionth. All perturbing forces of the first order
are, therefore, of the order of magnitude of only one-millionth of the
full force, even when the speed of propagation is as small as that of light.
The simplest case is when the common motion of the Sun and Earth is
perpendicular to the plane of the orbit. Then 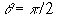 ,
all round the orbit, and
,
all round the orbit, and
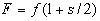 ,
(5)
,
(5)
showing increase in the force of attraction of 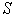 on
on 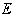 of
one two-millionth part, without alteration of direction or variation in
tile orbit
of
one two-millionth part, without alteration of direction or variation in
tile orbit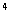 .
.
4 But Prof. Lodge tells me that our own particular Sun it
considered to move only 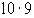 miles
per second. This 11 stupendously slow. The size of
miles
per second. This 11 stupendously slow. The size of 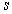 is
reduced to about 1/360 part of that in the text, and the same applies to
the corrections depending upon it.
is
reduced to about 1/360 part of that in the text, and the same applies to
the corrections depending upon it.
But when the common motion of the Sun and Earth is in their plane, в
varies from 0 to 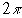 in a revolution,
so that the attraction on
in a revolution,
so that the attraction on 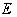 ,
whilst towards the Sun's centre, always undergoes a periodic variation
from
,
whilst towards the Sun's centre, always undergoes a periodic variation
from
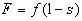 (6)
(6)
when 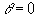 , to
, to
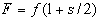 (7)
(7)
when 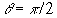 . The extreme variation
is, therefore,
. The extreme variation
is, therefore, 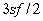 , according
to the data used. The result is a slight change in the shape of the orbit.
, according
to the data used. The result is a slight change in the shape of the orbit.
But, to be consistent, having made v finite by certain suppositions,
we should carry out the consequences more fully, and allow not merely for
the change in the Newtonian law, as above, but for the force brought in
by the finiteness of v which is analogous to the "electromagnetic
force." This is very small truly, but so is the above change in the Newtonian
law, and since they are of the same order of magnitude, we should also
count the auxiliary force. Call it 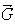 .
Then
.
Then
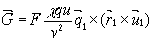 ,
(8)
,
(8)
where 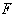 is as before,
in (2) above,
is as before,
in (2) above, 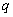 is the actual
speed of the Earth (not the same as u), and in the third vectorial
factor
is the actual
speed of the Earth (not the same as u), and in the third vectorial
factor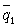 ,
, 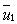 and
and 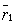 ,
are unit vectors drawn parallel to the direction of the Earth's motion,
of the Sun's motion, and from the Sun to the Earth. We see at once that
the order of magnitude cannot be greater than that of the departure of
,
are unit vectors drawn parallel to the direction of the Earth's motion,
of the Sun's motion, and from the Sun to the Earth. We see at once that
the order of magnitude cannot be greater than that of the departure of 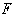 from
from 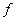 before
considered, because
before
considered, because 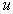 and
and 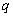 will
be of the same order, at least when
will
be of the same order, at least when 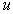 is
big. As for
is
big. As for 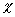 , it
is simply a numerical factor, which cannot exceed 1, and is probably 2/3
, it
is simply a numerical factor, which cannot exceed 1, and is probably 2/3
The simplest case is when the motion 'of the Sun is perpendicular to
the orbit of the Earth. Then
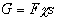 (9)
(9)
gives the tensor5 or size of the auxiliary force. It is radial,
but
5 Heaviside uses
the word "tensor" fur the magnitude of the force vector (0. D. J.).
outwards, so that the result is merely to reduce the size of the previous
correction, viz., the difference of 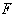 from
from 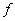 in
the same motional circumstances.
in
the same motional circumstances.
But when the line of motion of Sun is in the plane of the orbit, the
case is much more complicated. The force 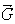 is
neither constant (for the same distance) nor radial, except in four positions,
viz., two in the line of motion of the Sun, when the auxiliary force vanishes,
and two when
is
neither constant (for the same distance) nor radial, except in four positions,
viz., two in the line of motion of the Sun, when the auxiliary force vanishes,
and two when 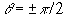 , when it
is greatest. But this force is still in the plane of the orbit, which is
an important thing, and is, moreover, periodic, so that the tangential
component is as much one way as the other in a period.
, when it
is greatest. But this force is still in the plane of the orbit, which is
an important thing, and is, moreover, periodic, so that the tangential
component is as much one way as the other in a period.
All we need expect, then, so far as I can see from the above considerations,
are small perturbations due to the variation of the force of gravity in
different directions, and to the auxiliary force. Of course, there will
be numerous minor perturbations
If variations of the force of the size considered above are too small
to lead to observable perturbations of motion, then the striking conclusion
is that the speed of gravity may even be the same as that of light. If
they are observable, then, if existent, they should turn up, but if non-existent
then the speed of gravity should be greater. Furthermore, it is to be observed
that there may be other ways of expressing the propagation of gravity.
But I am mindful of the good old adage about the shoemaker and his last,
and am, therefore, reluctant to make any more remarks about perturbations.
The question of the ether in its gravitational aspect must be faced, however,
and solved sooner or later, if it be possible. Perhaps, therefore, my suggestions
may not be wholly useless.
________
Web-публикация: guts@univer.omsk.su, Omsk, December 15, 2001.

